Calcolo, Supercalcolo e Montessori
Da un punto di vista un po’ inusuale, quello di chi si occupa di rendere visibili i numeri prodotti in grande quantità sui supercomputer del Centro Svizzero di Calcolo Scientifico (CSCS), getteremo uno sguardo su alcuni aspetti poco considerati della matematica: l’importanza dell’immaginazione e dei sensi, la matematica come scienza delle configurazioni ma anche sull’importanza del provare ed esplorare in prima persona per capire e comprendere.
Molte idee che si ritrovano nel mondo del supercalcolo sono strettamente correlate alle idee di Maria Montessori. Non solo, anche in ambiti scolastici più tradizionali la matematica può essere affrontata in maniere più consone al funzionamento della nostra mente.
Certo, si sa che la matematica non è amata, ma quello che gli studenti odiano spesso non è la matematica, ma l’esperienza dell’insegnamento della matematica. E questa forse si può cambiare.
Il relatore
Mario Valle aiuta ricercatori e scienziati a estrarre il significato nascosto nei numeri prodotti in quantità dai supercomputer del Centro Svizzero di Calcolo Scientifico (CSCS). Per far questo si avvale di tecniche e strumenti di visualizzazione per reclutare quella parte del nostro cervello capace di riconoscere configurazioni e regolarità quasi senza sforzo cosciente. Strumenti che in definitiva “concretizzano l’astrazione” dei modelli matematici. Ed ecco perché non ci sono solo scienza e numeri nelle sue giornate. Tramite suo figlio, che ha frequentato una scuola Montessori, è arrivato a scoprire come questi due mondi apparentemente distanti, quello del progetto Montessori e quello del supercalcolo, in realtà abbiano molti, interessanti punti di contatto che meritano di essere studiati e approfonditi.
Il convegno
Questo lavoro è stato presentato nell’ambito del convegno: “Viaggio attraverso i numeri” tenutosi a Genova mercoledì 18 dicembre 2013 presso il Salone di Rappresentanza di Palazzo Tursi.
La presentazione

Buon pomeriggio!

Chi di voi non ha sentito definire la matematica come una materia arida, difficile.

Chi di voi non ha sofferto durante le lezioni di matematica a scuola? Chi di voi non ricorda terribili professori di questa materia? Ovviamente gli insegnanti di matematica qui presenti non rientrano in questa categoria.

Chi di voi, come Guccini, non si è mai rifugiato nell’autogiustificazione: “Tanto non sono portato per la matematica”, oppure “Io proprio dei numeri non ci capisco niente”?

Invece questo pomeriggio voglio convincervi che un’altra matematica è possibile e che voi che insegnate in una scuola Montessori o voi genitori che avete figli che frequentano tali scuole potete guardare a come fanno matematica con un altro occhio e addirittura vantarvi della modernità dei materiali e soprattutto delle idee che li animano.

Bene, è venuto il momento di presentarmi. Io lavoro al Centro Svizzero di Calcolo Scientifico,…

…dove sono ospitati alcuni dei calcolatori più potenti al mondo, come “Piz Daint” che è il sesto per potenza in assoluto. …

… Queste macchine producono numeri e calcoli a getto continuo. Numeri che devono essere compresi, numeri che devono aiutare gli scienziati nel loro lavoro di studio della natura. Numeri che, come diceva il fisico e premio Nobel Eugene Wigner, mostrano ogni giorno l’“irragionevole efficacia della matematica nelle scienze naturali”.

Numeri e calcoli con cui per esempio si simula la formazione di una galassia. Numeri che rendiamo visibili per facilitare la comprensione del fenomeno simulato da parte dello scienziato.

Numeri che permettono, come con un potentissimo microscopio, di vedere l’infinitamente piccolo, come qui, dove viene reso visibile il comportamento della proteina precursore dell’Alzheimer che tesse le sue mortali fibrille che uccideranno i neuroni.

Numeri per comprendere fenomeni all’apparenza più frivoli, come lo studio del nuoto di una medusa.
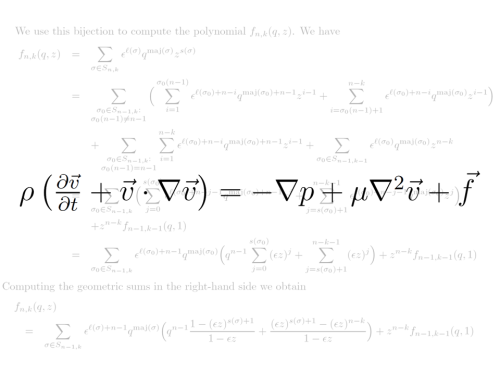
Dietro queste belle immagini, dietro ogni simulazione e calcolo eseguito sui supercomputer, la matematica la fa da padrone, ma a noi che lavoriamo al centro di calcolo più che la bellezza asettica delle formule o l’astrazione dei simboli interessa…

… come prendere queste formule e trasformarle in qualcosa che il calcolatore possa comprendere. Non solo, alla fine del calcolo o della simulazione dobbiamo riuscire a rendere comprensibili i risultati numerici in modo che stimolino la nascita di nuove idee e l’acquisizione di nuove conoscenze.
E come ci riusciamo?

Ci riusciamo spesso utilizzando la parte più creativa del cervello, mica la parte sinistra, quella razionale e matematica, quella delle formule e dei numeri. Strano, vero?

Spesso ci riusciamo scarabocchiando schemi incomprensibili su una lavagna, dove cerchiamo di concretizzare qualche idea che abbiamo per la testa per discuterne con un collega.
Come la lavagna del mio ufficio sulla quale ha lasciato un suo contributo anche mio figlio…

…che è stato la causa del mio incontro col mondo Montessori. Un mondo di cui all’inizio non sapevo nulla, la scelta della scuola è stata un po’ un atto di fede, ma poi sentendo i suoi racconti, osservando e leggendo…

…ho trovato tanti paralleli tra le idee montessoriane e il mio lavoro, tra quello che è comune in un ambiente scientifico e quello che ho visto nell’ambiente di una scuola Montessori. Se volete saperne di più, c’è un mio articolo sul Quaderno Montessori n. 100.
Oggi voglio però concentrarmi su uno di questi aspetti in comune, e lo faccio partendo da un ricordo della mia di scuola elementare.
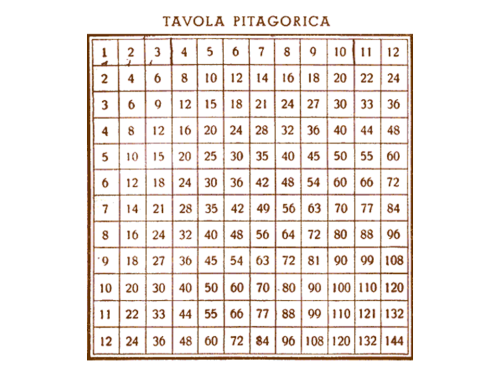
Le tabelline.
Chi non ricorda la tavola pitagorica stampata alla fine dei venerabili Quaderni Pigna? Era l’unica distrazione a disposizione durante le spiegazioni noiose.

Invece alla scuola di mio figlio trovo una tavola di legno con dei chiodi e un filo di lana. La tavoletta o mandala delle tabelline.

La tabellina del due? Conto uno due e avvolgo il filo. …

…Uno, due e avvolgo il filo. …

… Alla fine ho un pentagono.

La tabellina del tre? Uno due tre e avvolgo il filo. …

… Così via e mi ritrovo con una stella a dieci punte.

La tabellina del quattro? …

… La stella è ora a cinque punte.

La tabellina del cinque è tutta sua, è una linea.

La tabellina del sei. …

… Guarda guarda, la stessa stella della tabellina del quattro. Ci sarà forse una connessione tra 4 e 6?

Tabellina del sette. …

… Come la stella della tabellina del tre. Forse c’è una connessione tra 7 e 3 come c’era fra 6 e 4.

Tabellina dell’8. Mi aspetto la stessa struttura della tabellina del due. …

… Infatti!

In che cosa siamo incappati? Nella materializzazione di un qualcosa di astratto come la lista dei multipli dei numeri naturali. Anche se, strettamente parlando, questo non è tra i materiali originali Montessori, i principi sono quelli. Abbiamo trasformato un lavoro puramente intellettuale di traduzione di simboli in significato in un lavoro di riconoscimento di forme. Questo ci porta dritto dritto…

…al moderno movimento che vuole aggiornare la definizione di matematica dal tradizionale «la scienza dello spazio e del numero» in «la scienza delle configurazioni».

Non è però una novità. Già nel 1940 il matematico Godfrey Hardy diceva che «Un matematico, come un pittore o un poeta, è un creatore di schemi. Se i suoi schemi sono più permanenti dei loro, è perché sono fatti di idee.»
C’è di più. Già Évariste Galois cambiò il volto dell'algebra concentrandosi non più su numeri o funzioni, bensì su strutture, in cui gli oggetti matematici non erano presi nella loro singolarità, bensì nel loro insieme e uniti da legami che strutturano questi insiemi.

Le strutture sono importanti e noi ci siamo evoluti per riconoscerle a colpo d’occhio. Riconoscere strutture caratteristiche attorno a noi può fare la differenza tra la vita e la morte quando si tratta di riconoscere lo schema delle macchie sul manto di un predatore in agguato nascosto nell’ombra sotto un albero.

Oggi noi non abbiamo più bisogno di difenderci dalle bestie feroci, ma la capacità di riconoscere schemi e strutture a colpo d’occhio è rimasta.

Ed è proprio questa capacità che io uso nella visualizzazione scientifica per aiutare i ricercatori a capire i numeri che producono. A volte bastano dei semplici grafici per cogliere immediatamente le strutture nascoste nei loro dati.

Ma, ditemi, che differenza c’è con quello che fa un bambino che lavora con il materiale Montessori delle marchette? Anche lui sta creando configurazioni a partire dall’idea astratta di numero! E usa il riconoscimento di strutture anziché il richiamo di nozioni memorizzate per esplorare il concetto di pari e dispari.

E in questa scuola tradizionale non solo materializzano la linea dei numeri, questi bambini la creano con tutto il corpo, non solo con la testa. Creano una configurazione: la linea dei numeri.
In più, come vedremo, studi dicono che il bambino sin da piccolo si costruisce nella mente – immagina – la linea dei numeri.
Ma per costruirsi un’immagine mentale della linea dei numeri serve vederla! Noi costruiamo immagini mentali, ma riusciamo a immaginare solo ciò che ci entra attraverso gli occhi.

Ed ecco perché qui troviamo il serpente del mille e bambini che mettono freccette con i valori. Nel loro lavoro occupano tutto il corridoio di ingresso della Casa dei Bambini e anche qui usano l’intero corpo, non solo la testa per immaginare un insieme di mille numeri. Possiamo dire che è la stessa idea anche se con differenti etichette pedagogiche.

Quando vedete una bambina lavorare con i fuselli, annodandoli assieme, dovete pensare che non solo acquisisce il concetto di numero come composto da unità legate assieme, ma il movimento delle mani, il dover fare il nodo aiuta ad acquisire il concetto con tutto il corpo.
Oltre ad imparare a fare i nodi, che non guasta.

Mia moglie insegna in una scuola tradizionale e utilizza il «Metodo Analogico-Intuitivo» di Camillo Bortolato, che, pur non essendo assolutamente legato a Montessori, ne condivide alcune idee.
Ecco per esempio che cosa dice riguardo all’importanza delle strutture per l’insegnamento della matematica. Il dato di quantità non lo rileviamo dalla percezione delle cose, ma dalla posizione di ciascuna, ovvero dallo schema soggiacente. I bambini bravi intuiscono l'importanza di questo ordine: è il loro segreto. Anche qui strutture e configurazioni.

Ma torniamo ai materiali. Abbiamo visto come materializzano un’astrazione attraverso la creazione di strutture. Stesso concetto, strutture differenti. Così è più probabile che il concetto si fissi nella mente. Non solo, ma è come in un’azione militare: la matematica non viene attaccata frontalmente, ma girandoci attorno. Così viene conquistata quasi senza accorgersene.

Del resto è quello che si fa per aiutare la comprensione dei dati con la visualizzazione scientifica: si rappresenta la stessa quantità in più maniere differenti sperando che almeno uno dei modi faccia scattare nella testa del ricercatore la comprensione cercata. Qui per esempio si rappresenta l’altitudine di un modello topografico in due maniere: come vera e propria altezza della superficie tridimensionale che rappresenta il terreno e utilizzando una scala di colori.

Questa ridondanza è differente dall’aggiungere orpelli inutili o solamente decorativi.
Perché i materiali non rendono più simpatico l’apprendimento usando colori e disegnini? Perché dobbiamo sovraccaricare il sistema percettivo diluendo il concetto che stiamo passando in una marea di rumore e stimoli irrilevanti? La torre rosa è rosa proprio per questo motivo.
E poi, perché consideriamo i bambini delle scimmiette da sollazzare a tutti i costi? Impariamo invece a conoscere e rispettare le loro capacità, anche matematiche.

Questo purtroppo succede spesso anche nel mio campo. Ho ritagliato questa visualizzazione perché lo mostra chiaramente. Per rappresentare dei dati, qui sono addirittura solamente tre, dico tre, numeri li annega in un mare di dettagli decorativi inutili che non aiutano la percezione, non aiutano a cogliere il fenomeno che i numeri rappresentano. Inoltre, ho voluto ritagliare questa grafica non solo perché è “barocca”, è pure sbagliata! Qui i numeri crescono verso il basso contrariamente alle nostre aspettative.

Invece rappresentandoli in modo da trasmettere quello che i numeri rappresentano fa si che cogliamo senza sforzo il messaggio centrale: la fertilità negli Stati Uniti sta crollando verticalmente.

Del resto nella visualizzazione scientifica spesso si eliminano gli elementi non essenziali che ostacolano la comprensione dei dati. Per esempio in questa rappresentazione di un oligopeptide chiamato netropsina legato alla doppia elica del DNA, quest’ultima è rappresentata in maniera schematica con dei dischi al posto delle basi che la compongono.

Ma ritorniamo ai materiali. Se fate un giro in una qualsiasi scuola Montessori degna di questo nome, non vi stupirete di trovare le aule sempre ben ordinate. Non è mania, né un qualcosa fine a se stesso. È ricordare visivamente un aspetto della mente dei bambini. …

…Quale? Basta vedere questo bambino del nido rimettere in ordine da solo i materiali che ha usato. E l’ordine non è forse un concetto matematico?

Questo ordine e questa cura ci fanno capire quanto sia vera questa affermazione di Maria Montessori. In parole mie, non dobbiamo imboccare a forza i bambini con la matematica, dobbiamo solo trovare il cucchiaio adatto. In più, se fate attenzione, questa frase non parla di formule e teoremi. Parla di esattezza e ordine. Quindi forse il fine dell’insegnamento della matematica nelle scuole Montessori non sarà forgiare geni ma persone.

Andiamo avanti. Oltre che con gli occhi, la matematica che ho visto alle scuole Montessori è matematica che si fa con le mani. E non in una maniera qualsiasi, in una maniera scientificamente precisa.

Per esempio. Perché le aste numeriche si prendono così e non in mezzo che sarebbe più comodo? Perché le aste devono trasmettere un concetto geometrico che qui è la lunghezza. Prendendole in mezzo si trasmetterebbe solo il peso. E noi non siamo così bravi a distinguere e ordinare il peso così come lo siamo per le lunghezze.

Con le mani si materializza l’astrazione del teorema di Pitagora. Non si illustra un’idea astratta, non è un “sussidio didattico”. Questo materiale di sviluppo crea un ponte materiale tra il fare e l’idea astratta.

Le mani che nei secoli passati erano la base dell’aritmetica e dei calcoli di tutti i giorni.

Ma anche osservando le mani di una maestra Montessori ci rendiamo conto che sono una parte fondamentale del suo lavoro. Non si muovono in obbedienza a qualche rito esoterico, no, le mani parlano e strutturano, danno un ordine a quello che stanno presentando.

Così guardando i bambini che lavorano con i materiali di sviluppo, rendiamoci conto che stanno “pensando con le mani”, non stanno mica giocando!
Mani e matematica ci svelano un altro segreto riguardo all’efficacia dell’insegnamento della matematica in una scuola Montessori e lo fanno addirittura in sala da pranzo.

In una situazione del genere quasi tutte le mamme direbbero “Stai attenta!” Ma ci dimentichiamo che questa avvertenza è un’astrazione. Che cosa vuol dire “stai attenta”? Che devo fare? Che significa?
Invece fin dal nido Montessori la maestra dice: “Violetta, prendi il piatto con due mani, così lo porti meglio fino al tavolo”.
La stessa cosa accade con una formula come questa. La formula del cubo del binomio è un’astrazione, è un modo rapido ma astratto di spiegare…

…quello che con le mani capisco in cinque minuti! E me lo ricordo pure. Non siamo all’università! Non è necessario mettere davanti l’astrazione a tutti i costi!

Quindi astrazioni materializzate. Lo scriveva il premio Nobel Richard Feynman sulla sua lavagna poco prima di morire: «Ciò che non posso creare, non posso capire». Bella lezione.
Anche uno che scrive «cose da studiare» sapendo di stare per morire ci da una lezione potente.

Io non sono così fortunato. Posso tuttalpiù manipolare un modello sullo schermo, girarci intorno e guardarlo da diversi punti di vista. …

…Oppure gesticolare e costruire nell’aria schemi e strutture che chiariscano quello che ho in mente, rendendo in qualche modo concreto ciò che prima ho dovuto immaginare nella mia mente.

Che non è molto diverso da quello che fa un matematico di fronte a schemi e immagini come queste. …

…Tanto importante è questo modo di lavorare che il grande Hilbert ha scritto un intero libro su Geometria e Immaginazione. Se qualcuno mi dice che geometria non è matematica gli dico di andare a leggersi come la geometria si riconduce alla teoria dei gruppi, per esempio.

E allora ben vengano le manipolazioni degli incastri che si fanno alla Casa dei Bambini. In un senso molto concreto questi bambini fanno matematica e geometria.

E tornando all’immaginazione, alle immagini mentali, parliamo della linea dei numeri come la immagina un bambino.
Quando a maggio scorso Francesco mi ha detto: “Sai che so contare fino a mille?” “Molto interessante, fammi sentire”. “Uno, due, tre, quattro, mille”. Mi è venuto in mente che avevo letto…

…un articolo di due psicologi che dimostrano come la linea dei numeri nella mente di un bambino sia rada all’inizio e via via più addensata dalla parte dei numeri più grandi, proprio come ha fatto Francesco in maniera esagerata. Gli autori aggiungono poi che più questa linea diviene uniforme, più il bambino acquista capacità di memorizzazione dei numeri.

Ma avete mai guardato con attenzione il lavoro che in una scuola Montessori i bambini fanno col serpente del mille? Etichette addensate all’inizio, poi un po’ più rade e poi sempre più rade per i numeri grandi. Notate? Esattamente al contrario di come si svolge la linea dei numeri nella testa del bambino. Come se questo lavoro aiutasse a stendere e uniformare la linea mentale dei numeri. Un caso? Non credo, è a mio avviso un’altra delle intuizioni a cui la Dottoressa era arrivata cento anni fa.

E come finisce la storia di Francesco? L’ho incontrato di nuovo ad ottobre. Nel frattempo aveva incominciato a usare alcuni materiali Montessori a casa. Gli ho ricordato quello che mi aveva detto, come sapeva contare fino a mille. Lui mi guarda con commiserazione e facendo il gesto con le mani di tenere il cubo del mille mi dice: “Ma no! Il mille è pesante”

Un altro aspetto matematico che ho in comune con i cuccioli del nido è l’esplorazione. Qui possiamo trovare bambini che giocano col cestino dei tesori di Elinor Goldschmied. Certo non fanno matematica. Svuotano prendono combinano cercano. Non si stancano mai. Ma la cosa che mi ha colpito è che prima di tutto esplorano, senza un’idea preconcetta di quello che troveranno. Non solo, non c’è una maniera “giusta” o “sbagliata” di esplorare, non si possono dare voti.

Ed è quello che devo fare molto spesso. Non so che cosa troverò. Combino tutti i numeri che ho generato sperando che qualche combinazione mi faccia drizzare le orecchie.
Per esempio qui ho sei variabili per ognuno di diecimila cristalli. Li provo a combinare due a due e una combinazione attira la mia attenzione. …

…Per cui rappresento in modo differente queste quantità ed ecco che mostrano una relazione più interessante. L’esplorazione suggerisce delle nuove ipotesi.

Esplorare è fondamentale per la scienza. Esplorare è il modo per catturare l’essenza di un problema e quindi per porre le domande giuste.
Il grande statistico John Tukey (che tra l’altro ha coniato tanti termini ora di uso comune come bit e software) ha addirittura inventato una nuova branca della statistica chiamata appunto «Exploratory Data Analysis».

Se la matematica diventa così, un gioco di esplorazione, allora anche inventarsi queste lenzuolate di somme è divertente e spinge a creare cose non previste dai programmi scolastici. …

…Vedete il quadernino? Questo bambino, che ha usato il metodo di Bortolato alla scuola di Solbiate con una maestra montessoriana nell’animo, si è inventato un meccanismo per non perdere il filo durante somme così lunghe. E così è arrivato a costruire una struttura ad albero, un qualcosa che in informatica trovi dappertutto.

Se si è liberi di esplorare non c’è limite a che cosa si può trovare.
Questo bel documento racconta come in una scuola Montessori olandese…

…i bambini hanno scoperto che le differenze tra i quadrati dei numeri interi sono sempre dei numeri dispari e che la differenza tra le differenze è sempre 2. Poi si sono chiesti: e come si comportano i cubi? La differenza tra le differenze delle differenze è sempre 6 questa volta. E per le quarte potenze? E le quinte?
Lasciati liberi di esplorare nulla li ferma. Leggiamo quello che diceva la loro maestra. …

…“Mai fatti tanti calcoli come in questi giorni; mai visti i bambini esigere così tanta accuratezza da loro stessi poiché il più piccolo errore avrebbe distrutto la regolarità dello schema con i numeri finali, tutti numeri pari. Fu interessante vedere che se c’era stato un errore i bambini lo realizzavano da soli perché il numero risultante non poteva occupare nessun posto nello schema.”
Notate che anche qui viene fuori lo schema, mica le formule o le regole. E i risultati che derivano dalla libertà di esplorare.

Un librettino che vi consiglio di leggere è: Contro l’ora di matematica di Paul Lockhart. L’autore si chiede come mai a scuola non si fa matematica e come invece dovrebbe essere avvicinata agli studenti. Vi ho trovato un aneddoto molto interessante. …

…Paul chiese ai suoi allievi di dimostrare che in ogni cerchio tutti i triangoli inscritti che hanno un lato sul diametro sono rettangoli.

Che scoperta! Ogni libro di geometria ne riporta la dimostrazione. Ma Paul non vuole studenti pappagalli, vuole esseri pensanti. E così un suo allievo, dopo aver esplorato e provato, arriva a una nuova dimostrazione…

…basata sulla simmetria.

Ancora una volta voglio sottolineare che a vedere così i problemi ci arrivi se hai nella mente i pezzi da costruzione che hai immagazzinato manipolando triangoli e cerchi reali e materiali.

Certo, mi direte, sono piccole scoperte. Non disdegniamole, sono comunque scoperte di cui andar fieri. Poi notate che si fa tesoro delle risposte solo se ci si è scontrati autonomamente con le domande. Tagliare il momento della domanda, della curiosità, significa togliere significato. E aumentare il rischio che l’apprendimento resti fugace e non lasci traccia sul lungo periodo.

Il librettino di Paul Lockhart si apre con questa citazione di Antoine de Saint-Exupéry che io traduco così: prima di formule e teoremi facciamo appassionare alla materia! Non siamo all’università, facoltà di matematica dove si presume uno ci capiti perché gli piace la matematica. Siamo nelle scuole dell’obbligo, dove devo appassionare i ragazzi, che poi seguiranno ognuno la propria strada.

Raccontiamo storie, facciamo vedere che cosa fa un matematico nella vita! Ci sono storie più avvincenti di un giallo, come la storia della dimostrazione della congettura di Poincaré dove c’è un premio da un milione di dollari che è stato rifiutato.

Se ci pensate una bella storia cattura la vostra attenzione e la vedete letteralmente nella mente. E questo gli scienziati del passato lo sapevano. Raccontavano le loro scoperte come una storia o un dialogo. Perché noi siamo “programmati per le storie”.

Invece quello che succede alle lezioni di matematica lo racconta appunto un romanzo, “Il teorema del pappagallo”: durante le lezioni di matematica non si parlava mai di esseri umani.
A Varese Nadia Tunesi, la maestra di mio figlio, prendendo spunto proprio da questo romanzo, aveva organizzato delle brevi rappresentazioni su Talete Fibonacci Tartaglia e Pitagora con tanto di mantello e la ricostruzione della scuola pitagorica. Risultato? Ragazzi entusiasti e concetti matematici ben scolpiti nella loro mente.
E Maria Montessori? Certo lei non aveva mai fatto questo, ma aveva detto: “Ciò che [il bambino] apprende deve essere interessante, deve affascinarlo: bisogna offrirgli cose grandiose: per cominciare, offriamogli il Mondo” (Dall’Infanzia all’Adolescenza, cap. V pag. 45) ed è proprio questo che ha fatto la maestra!

Pensate come sarebbe avvincente una scuola in cui l’insegnante di matematica parlasse per esempio di simmetrie mostrando questa foto dell’Alhambra di Granada, quella di storia vi si agganciasse e parlasse della dominazione araba in Andalusia, quello di arte dell’arte islamica, quello di geografia della penisola iberica. E poi si può parlare di religione, convivenza, storia della matematica… Ecco che la matematica non sarebbe più un corpo estraneo nella giornata scolastica. In una scuola Montessori questo rischio non si corre, è proprio l’educazione cosmica che unifica e lega tutto.

Del resto se ne parla anche in Psicoaritmetica, dove questo allargare gli orizzonti si mostra far bene anche alla matematica stessa.

A questo punto sorge spontanea la domanda: “Va bene, la matematica si può insegnare in un altro modo, ma a cosa serve studiare matematica?”

A passare esami e interrogazioni? Che obiettivo misero! Se è così, dice bene Paul Lockhart che bisogna abolire l’ora di matematica perché in quelle ore non si fa matematica.

Serve per diventare tutti dei matematici? No, ma per riuscire a sentire che la matematica “è alla mia portata”, anche se poi preferisco studiare un’altra cosa.

Serve sicuramente per non “prendere per oro colato” tutto quello che contiene numeri, per poi farsi fregare da offerte mirabolanti come questa.

E per non fare figure barbine come queste.

Un po’ di luce sulla questione ce la può dare Maria Montessori che addirittura nel 1939 ne “La mente del bambino” scrive queste parole. Ma secondo voi parla di qualcosa specifico della matematica oppure di quello che dovrebbe fare ogni essere pensante e libero?

Sul lungo periodo la matematica, il ragionamento matematico devono servire per diventare una persona che sa usare la matematica per leggere il mondo circostante, interpretarlo, e intervenire razionalmente su di esso. E questo inizia imparando a vedere nella matematica stessa le strutture, l’ordine e la logica dei suoi concetti ed argomenti.

Ecco allora qual è lo scopo della matematica: la comprensione e lo sviluppo umano.

Abbiamo visto la matematica come scienza delle configurazioni e bambini che fanno matematica proprio così. Abbiamo visto in pratica che «Ciò che posso creare, posso capire». Abbiamo visto come la libertà di esplorare spinge a fare della vera matematica.
Pensiamoci, così quando vedremo i materiali di una scuola Montessori non li liquideremo più con supponenza come cose vecchie e superate. Ammiriamo invece la lungimiranza e l’intuito di una scienziata di quasi cento anni fa.
Grazie per l’attenzione!
![La locandina dell’incontro [La locandina dell'incontro]](invitoGenova2013-small.png)